評價此頁
★ ★ ★ ★ ★

分散式自動微分設計#

創建於：2019 年 11 月 12 日 | 最後更新於：2021 年 9 月 3 日

本文件將介紹分散式自動微分的詳細設計，並深入探討其內部機制。在繼續閱讀之前，請確保您已熟悉 自動微分機制 和 分散式 RPC 框架。

背景#

假設您有兩個節點，並且一個非常簡單的模型被劃分到這兩個節點上。這可以使用 torch.distributed.rpc 實現，如下所示：

import torch
import torch.distributed.rpc as rpc

def my_add(t1, t2):
  return torch.add(t1, t2)

# On worker 0:
t1 = torch.rand((3, 3), requires_grad=True)
t2 = torch.rand((3, 3), requires_grad=True)

# Perform some computation remotely.
t3 = rpc.rpc_sync("worker1", my_add, args=(t1, t2))

# Perform some computation locally based on remote result.
t4 = torch.rand((3, 3), requires_grad=True)
t5 = torch.mul(t3, t4)

# Compute some loss.
loss = t5.sum()

分散式自動微分的主要動機是為了能夠對這種分散式模型執行反向傳播，使用我們已經計算出的 loss，併為所有需要梯度的張量記錄適當的梯度。

前向傳播過程中的自動微分記錄#

PyTorch 在前向傳播過程中構建自動微分圖，該圖用於執行反向傳播。有關更多詳細資訊，請參閱 自動微分如何編碼歷史記錄。

對於分散式自動微分，我們需要在前向傳播過程中跟蹤所有 RPC 呼叫，以確保反向傳播能夠正確執行。為此，當我們執行 RPC 時，我們會將 send 和 recv 函式附加到自動微分圖中。

  • send 函式附加到 RPC 的源端，其輸出邊指向 RPC 輸入張量的自動微分函式。在反向傳播期間，此函式的輸入是從目標節點透過相應的 recv 函式接收的。

  • recv 函式附加到 RPC 的目標端，其輸入透過目標端使用輸入張量執行的操作來檢索。此函式的輸出梯度在反向傳播期間作為輸出傳送到源節點，傳遞給相應的 send 函式。

  • 每個 send-recv 對都被分配一個全域性唯一的 autograd_message_id，以唯一標識該對。這在反向傳播期間查詢遠端節點上的相應函式時非常有用。

  • 對於 RRef，每當我們呼叫 torch.distributed.rpc.RRef.to_here() 時，我們都會附加一個適當的 send-recv 對來處理涉及的張量。

例如，我們上面示例的自動微分圖將如下所示（為簡化起見，已排除 t5.sum()）：

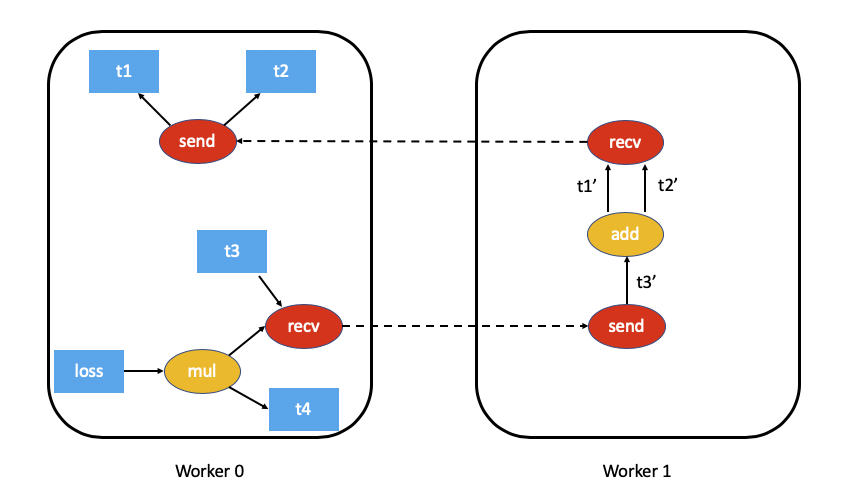
../_images/send_recv_functions.png

分散式自動微分上下文#

每個使用分散式自動微分的前向和反向傳播都會被分配一個唯一的 torch.distributed.autograd.context，並且該上下文有一個全域性唯一的 autograd_context_id。這個上下文會在需要時在每個節點上建立。

此上下文具有以下目的：

  1. 多個節點執行分散式反向傳播可能會在同一個張量上累積梯度，因此在我們有機會執行最佳化器之前，張量的 .grad 欄位將包含來自各種分散式反向傳播的梯度。這類似於多次在本地呼叫 torch.autograd.backward()。為了提供一種區分每次反向傳播的梯度的方法，梯度被累積在每個反向傳播的 torch.distributed.autograd.context 中。

  2. 在前向傳播期間，我們將每個自動微分過程的 send 和 recv 函式儲存在此上下文中。這確保我們持有自動微分圖中相應節點的引用，以保持其活動。此外，這使得在反向傳播期間更容易查詢相應的 send 和 recv 函式。

  3. 通常，我們還使用此上下文為每個分散式自動微分過程儲存一些元資料。


從使用者的角度來看，自動微分上下文的設定如下：

import torch.distributed.autograd as dist_autograd
with dist_autograd.context() as context_id:
  loss = model.forward()
  dist_autograd.backward(context_id, loss)

需要注意的是，您的模型的前向傳播必須在分散式自動微分上下文管理器中呼叫，因為需要一個有效的上下文才能確保所有 send 和 recv 函式被正確儲存，以便在所有參與節點上執行反向傳播。

分散式反向傳播#

本節將概述在分散式反向傳播過程中準確計算依賴關係的挑戰，並描述幾種（帶有權衡的）執行分散式反向傳播的演算法。

計算依賴關係#

考慮在單臺機器上執行的以下程式碼片段：

import torch
a = torch.rand((3, 3), requires_grad=True)
b = torch.rand((3, 3), requires_grad=True)
c = torch.rand((3, 3), requires_grad=True)
d = a + b
e = b * c
d.sum.().backward()

上述程式碼的自動微分圖將如下所示：

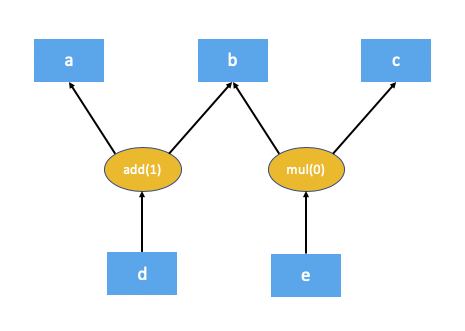
../_images/local_dependencies.png

作為反向傳播一部分的自動微分引擎執行的第一步是計算自動微分圖中每個節點的依賴項數量。這有助於自動微分引擎知道何時一個圖節點已準備好執行。對於 add(1) 和 mul(0)，方括號中的數字表示依賴項的數量。如您所見，這意味著在反向傳播期間，add 節點需要 1 個輸入，而 mul 節點不需要任何輸入（換句話說，不需要執行）。區域性自動微分引擎透過從根節點（在本例中為 d）遍歷圖來計算這些依賴項。

自動微分圖中某些節點可能不會在反向傳播中執行的事實給分散式自動微分帶來了挑戰。考慮這段使用 RPC 的程式碼：

import torch
import torch.distributed.rpc as rpc

a = torch.rand((3, 3), requires_grad=True)
b = torch.rand((3, 3), requires_grad=True)
c = torch.rand((3, 3), requires_grad=True)

d = rpc.rpc_sync("worker1", torch.add, args=(a, b))
e = rpc.rpc_sync("worker1", torch.mul, args=(b, c))
loss = d.sum()

上述程式碼的關聯自動微分圖將是：

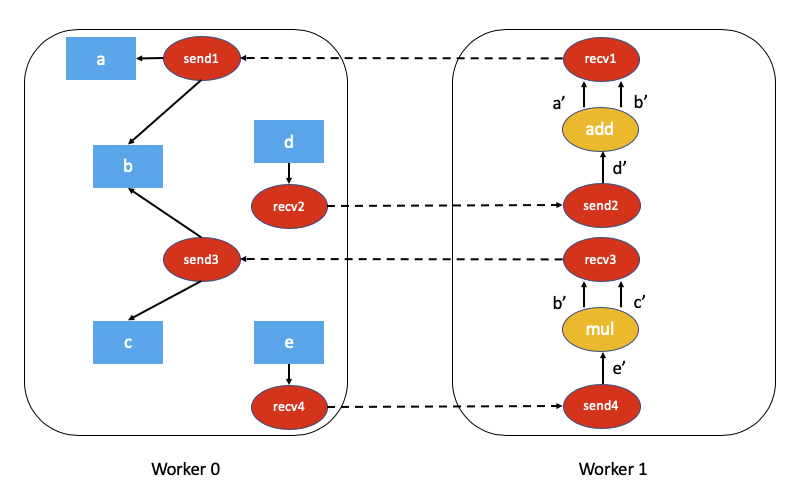
../_images/distributed_dependencies.png

計算這個分散式自動微分圖的依賴關係更具挑戰性，需要一些開銷（無論是計算還是網路通訊）。

對於效能敏感的應用，我們可以避免大量開銷，假設每個 send 和 recv 函式在反向傳播中是有效的（大多數應用不會執行不使用的 RPC）。這簡化了分散式自動微分演算法，並且效率更高，但代價是應用程式需要了解其侷限性。這個演算法稱為 FAST 模式演算法，下面將詳細描述。

在一般情況下，並非每個 send 和 recv 函式在反向傳播中都必須是有效的。為了解決這個問題，我們提出了一個 SMART 模式演算法，將在後續部分進行描述。請注意，目前僅實現了 FAST 模式演算法。

FAST 模式演算法#

此演算法的關鍵假設是，在執行反向傳播時，每個 send 函式都有一個依賴項為 1。換句話說，我們假設我們將從另一個節點透過 RPC 接收到梯度。

演算法如下：

  1. 我們從擁有反向傳播根節點的 worker 開始（所有根節點必須是本地的）。

  2. 查詢當前 分散式自動微分上下文 的所有 send 函式。

  3. 從提供的根節點和我們檢索到的所有 send 函式開始，在本地計算依賴關係。

  4. 計算完依賴關係後，使用提供的根節點啟動本地自動微分引擎。

  5. 當自動微分引擎執行 recv 函式時，recv 函式透過 RPC 將輸入梯度傳送到相應的 worker。每個 recv 函式都知道目標 worker ID，因為它是在前向傳播過程中記錄的。recv 函式還會將 autograd_context_id 和 autograd_message_id 傳送到遠端主機。

  6. 當在遠端主機上收到此請求時，我們使用 autograd_context_id 和 autograd_message_id 來查詢相應的 send 函式。

  7. 如果這是 worker 第一次收到給定 autograd_context_id 的請求，它將按照上述第 1-3 點在本地計算依賴關係。

  8. 在 6. 中檢索到的 send 函式隨後將被加入到該 worker 的本地自動微分引擎的執行佇列中。

  9. 最後，我們不是將梯度累積到張量的 .grad 欄位中，而是為每個 分散式自動微分上下文 分別累積梯度。梯度儲存在 Dict[Tensor, Tensor] 中，它本質上是一個從張量到其關聯梯度的對映，並且可以使用 get_gradients() API 檢索此對映。


作為一個例子，下面是包含分散式自動微分的完整程式碼：

import torch
import torch.distributed.autograd as dist_autograd
import torch.distributed.rpc as rpc

def my_add(t1, t2):
  return torch.add(t1, t2)

# On worker 0:

# Setup the autograd context. Computations that take
# part in the distributed backward pass must be within
# the distributed autograd context manager.
with dist_autograd.context() as context_id:
  t1 = torch.rand((3, 3), requires_grad=True)
  t2 = torch.rand((3, 3), requires_grad=True)

  # Perform some computation remotely.
  t3 = rpc.rpc_sync("worker1", my_add, args=(t1, t2))

  # Perform some computation locally based on remote result.
  t4 = torch.rand((3, 3), requires_grad=True)
  t5 = torch.mul(t3, t4)

  # Compute some loss.
  loss = t5.sum()

  # Run the backward pass.
  dist_autograd.backward(context_id, [loss])

  # Retrieve the gradients from the context.
  dist_autograd.get_gradients(context_id)

帶有依賴關係的分散式自動微分圖將如下所示（為簡化起見，已排除 t5.sum()）：

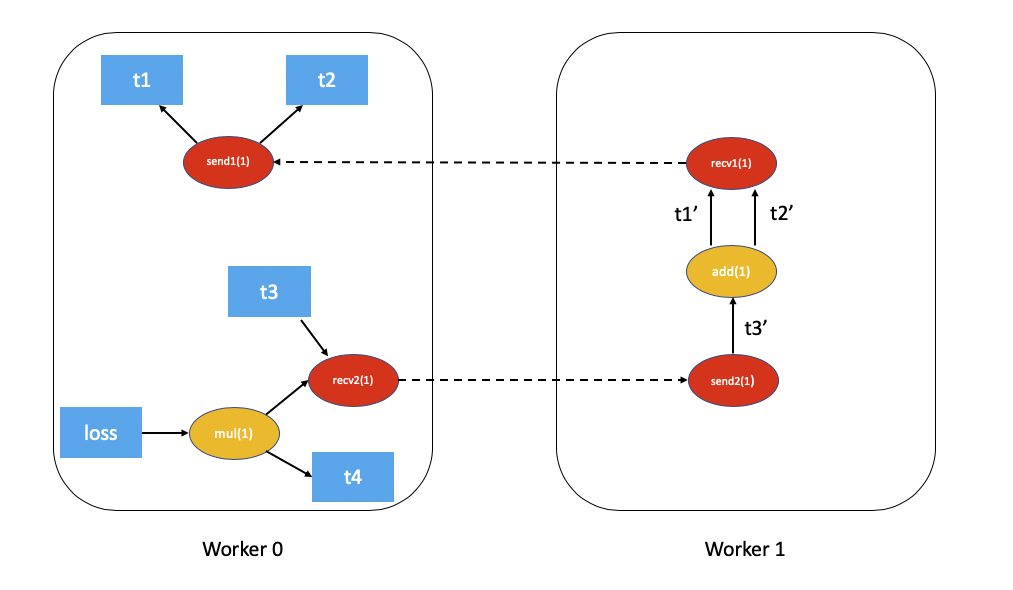
../_images/distributed_dependencies_computed.png

應用於上述示例的 FAST 模式演算法 將如下所示：

  1. 在 Worker 0 上，我們從根節點 loss 和 send1 開始計算依賴關係。結果是 send1 被標記為具有 1 的依賴性，而 Worker 0 上的 mul 被標記為具有 1 的依賴性。

  2. 現在，我們在 Worker 0 上啟動本地自動微分引擎。我們首先執行 mul 函式，將其輸出累積在自動微分上下文中作為 t4 的梯度。然後，我們執行 recv2，它將梯度傳送到 Worker 1。

  3. 由於這是 Worker 1 第一次收到有關此反向傳播的訊息，因此它開始計算依賴關係，並相應地標記 send2、add 和 recv1 的依賴關係。

  4. 接下來，我們將 send2 加入到 Worker 1 的本地自動微分引擎的佇列中，該引擎隨後執行 add 和 recv1。

  5. 當執行 recv1 時，它將梯度傳送到 Worker 0。

  6. 由於 Worker 0 已經為這個反向傳播計算了依賴關係，它只是在本地加入並執行 send1。

  7. 最後，t1、t2 和 t4 的梯度將累積在 分散式自動微分上下文 中。

SMART 模式演算法#

該演算法的完整細節仍在開發中，但有關其大致思想，您可以參考 RFC 中的 **分散式自動微分演算法 SMART 模式** 部分。

分散式最佳化器#

DistributedOptimizer 的工作原理如下：

  1. 接受一個要最佳化的遠端引數列表（RRef）。這些也可以是包裝在本地 RRef 中的本地引數。

  2. 接受一個 Optimizer 類作為本地最佳化器，在所有不同的 RRef 所有者上執行。

  3. 分散式最佳化器在每個 worker 節點上建立一個本地 Optimizer 例項，並持有指向它們的 RRef。

  4. 當呼叫 torch.distributed.optim.DistributedOptimizer.step() 時，分散式最佳化器使用 RPC 來遠端執行所有適當的遠端 worker 上的本地最佳化器。必須將分散式自動微分 context_id 作為輸入提供給 torch.distributed.optim.DistributedOptimizer.step()。這被本地最佳化器用來應用儲存在相應上下文中的梯度。

  5. 如果多個併發的分散式最佳化器正在更新 worker 上的同一組引數，這些更新將透過鎖進行序列化。

簡單的端到端示例#

將所有內容整合在一起，下面是一個使用分散式自動微分和分散式最佳化器的簡單端到端示例。如果將程式碼放在名為“dist_autograd_simple.py”的檔案中，可以使用命令 MASTER_ADDR="localhost" MASTER_PORT=29500 python dist_autograd_simple.py 來執行。

import torch
import torch.multiprocessing as mp
import torch.distributed.autograd as dist_autograd
from torch.distributed import rpc
from torch import optim
from torch.distributed.optim import DistributedOptimizer

def random_tensor():
    return torch.rand((3, 3), requires_grad=True)

def _run_process(rank, dst_rank, world_size):
    name = "worker{}".format(rank)
    dst_name = "worker{}".format(dst_rank)

    # Initialize RPC.
    rpc.init_rpc(
        name=name,
        rank=rank,
        world_size=world_size
    )

    # Use a distributed autograd context.
    with dist_autograd.context() as context_id:
        # Forward pass (create references on remote nodes).
        rref1 = rpc.remote(dst_name, random_tensor)
        rref2 = rpc.remote(dst_name, random_tensor)
        loss = rref1.to_here() + rref2.to_here()

        # Backward pass (run distributed autograd).
        dist_autograd.backward(context_id, [loss.sum()])

        # Build DistributedOptimizer.
        dist_optim = DistributedOptimizer(
        optim.SGD,
        [rref1, rref2],
        lr=0.05,
        )

        # Run the distributed optimizer step.
        dist_optim.step(context_id)

def run_process(rank, world_size):
    dst_rank = (rank + 1) % world_size
    _run_process(rank, dst_rank, world_size)
    rpc.shutdown()

if __name__ == '__main__':
  # Run world_size workers
  world_size = 2
  mp.spawn(run_process, args=(world_size,), nprocs=world_size)
在此頁面上
在 GitHub 上編輯
顯示原始碼
PyTorch 庫