


注意
跳轉至結尾 下載完整的示例程式碼。
簡介 || 張量 || Autograd || 構建模型 || TensorBoard 支援 || 訓練模型 || 模型理解
Autograd 的基礎#
創建於:2021 年 11 月 30 日 | 最後更新:2024 年 2 月 26 日 | 最後驗證:2024 年 11 月 05 日
請跟隨下面的影片或在 youtube 上觀看。
PyTorch 的 *Autograd* 功能是 PyTorch 在構建機器學習專案時之所以靈活且快速的原因之一。它能夠快速輕鬆地對複雜計算進行多次偏導數(也稱為 *梯度*)的計算。此操作是基於反向傳播的神經網路學習的核心。
Autograd 的強大之處在於它能在 *執行時* 動態追蹤你的計算,這意味著如果你的模型有決策分支,或者迴圈的長度直到執行時才能確定,計算仍然會被正確追蹤,並且你將獲得正確的梯度來驅動學習。這一點,再加上你的模型是用 Python 構建的事實,提供了比依賴於對更剛性結構的模型的靜態分析來計算梯度的框架更大的靈活性。
我們需要 Autograd 來做什麼?#
機器學習模型是一個*函式*,具有輸入和輸出。在本討論中,我們將輸入視為一個*i*維向量 \(\vec{x}\),其元素為 \(x_{i}\)。然後,我們可以將模型 *M* 表示為輸入的向量值函式:\(\vec{y} = \vec{M}(\vec{x})\)。 (我們將 M 的輸出值視為向量,因為 M 通常可能具有任意數量的輸出。)
由於我們主要將在訓練的上下文中討論 autograd,因此我們關心的輸出將是模型的損失。*損失函式* L(\(\vec{y}\)) = L(\(\vec{M}\)(\(\vec{x}\))) 是模型輸出的單個標量函式。此函式表達了模型的預測與特定輸入的*理想*輸出之間的差距。*注意:在此之後,我們將經常省略向量符號,只要上下文清晰即可 - 例如,* \(y\) 而不是 \(\vec y\)。
在訓練模型時,我們希望最小化損失。在理想的完美模型情況下,這意味著調整其學習權重 - 即函式的可調引數 - 以使所有輸入的損失為零。在實際世界中,這意味著一個迭代過程,即不斷調整學習權重,直到我們看到對於各種輸入都能獲得可接受的損失。
我們如何決定如何調整權重以及調整哪個方向?我們想*最小化*損失,這意味著使其關於輸入的第一個導數等於 0:\(\frac{\partial L}{\partial x} = 0\)。
但是,請記住,損失不是*直接*從輸入派生的,而是模型輸出(它是輸入的函式)的函式,\(\frac{\partial L}{\partial x}\) = \(\frac{\partial {L({\vec y})}}{\partial x}\)。根據微分學的鏈式法則,我們有 \(\frac{\partial {L({\vec y})}}{\partial x}\) = \(\frac{\partial L}{\partial y}\frac{\partial y}{\partial x}\) = \(\frac{\partial L}{\partial y}\frac{\partial M(x)}{\partial x}\)。
\(\frac{\partial M(x)}{\partial x}\) 是事情變得複雜的地方。模型輸出關於其輸入的偏導數,如果我們再次使用鏈式法則展開表示式,將涉及關於每個乘法的學習權重、每個啟用函式以及模型中的每個其他數學變換的許多區域性偏導數。每個此類偏導數的完整表示式是*每條可能路徑*透過計算圖的區域性梯度的乘積之和,該路徑以我們正在嘗試度量的變數的梯度為終點。
特別重要的是,關於學習權重的梯度對我們很重要 - 它們告訴我們*改變每個權重的方向*以使損失函式更接近零。
由於這些區域性導數的數量(每個導數對應於模型計算圖中的一條獨立路徑)往往隨著神經網路的深度呈指數級增長,因此計算它們的複雜性也隨之增加。這就是 autograd 發揮作用的地方:它會追蹤每個計算的歷史。你 PyTorch 模型中的每個計算出的張量都帶有其輸入張量和建立它的函式的歷史記錄。結合 PyTorch 中用於對張量進行操作的函式都具有計算自身導數的內建實現這一事實,這大大加快了計算學習所需的區域性導數的速度。
一個簡單的例子#
理論講了很多 - 但在實踐中使用 autograd 是什麼樣的?
讓我們從一個簡單的例子開始。首先,我們將進行一些匯入,以便我們可以繪製我們的結果
# %matplotlib inline
import torch
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import math
接下來,我們將建立一個包含 \([0, 2\pi]\) 區間內等距值的輸入張量,並指定 `requires_grad=True`。(與大多數建立張量的函式一樣,`torch.linspace()` 接受可選的 `requires_grad` 選項。)設定此標誌意味著在之後的每次計算中,autograd 都將累積該計算的輸出張量中的計算歷史。
a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
print(a)
tensor([0.0000, 0.2618, 0.5236, 0.7854, 1.0472, 1.3090, 1.5708, 1.8326, 2.0944,
2.3562, 2.6180, 2.8798, 3.1416, 3.4034, 3.6652, 3.9270, 4.1888, 4.4506,
4.7124, 4.9742, 5.2360, 5.4978, 5.7596, 6.0214, 6.2832],
requires_grad=True)
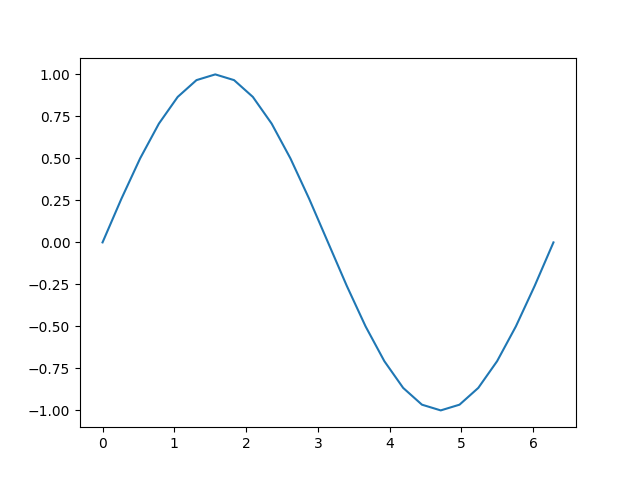
接下來,我們將執行一個計算,並繪製其輸出相對於其輸入的圖
[<matplotlib.lines.Line2D object at 0x7f49b5981750>]
讓我們仔細看看張量 `b`。當我們列印它時,我們會看到一個指示器,表明它正在追蹤計算歷史
print(b)
tensor([ 0.0000e+00, 2.5882e-01, 5.0000e-01, 7.0711e-01, 8.6603e-01,
9.6593e-01, 1.0000e+00, 9.6593e-01, 8.6603e-01, 7.0711e-01,
5.0000e-01, 2.5882e-01, -8.7423e-08, -2.5882e-01, -5.0000e-01,
-7.0711e-01, -8.6603e-01, -9.6593e-01, -1.0000e+00, -9.6593e-01,
-8.6603e-01, -7.0711e-01, -5.0000e-01, -2.5882e-01, 1.7485e-07],
grad_fn=<SinBackward0>)
這個 `grad_fn` 給了我們一個提示,當我們執行反向傳播步驟並計算梯度時,我們需要計算此張量所有輸入的 \(\sin(x)\) 的導數。
讓我們進行更多計算
tensor([ 0.0000e+00, 5.1764e-01, 1.0000e+00, 1.4142e+00, 1.7321e+00,
1.9319e+00, 2.0000e+00, 1.9319e+00, 1.7321e+00, 1.4142e+00,
1.0000e+00, 5.1764e-01, -1.7485e-07, -5.1764e-01, -1.0000e+00,
-1.4142e+00, -1.7321e+00, -1.9319e+00, -2.0000e+00, -1.9319e+00,
-1.7321e+00, -1.4142e+00, -1.0000e+00, -5.1764e-01, 3.4969e-07],
grad_fn=<MulBackward0>)
tensor([ 1.0000e+00, 1.5176e+00, 2.0000e+00, 2.4142e+00, 2.7321e+00,
2.9319e+00, 3.0000e+00, 2.9319e+00, 2.7321e+00, 2.4142e+00,
2.0000e+00, 1.5176e+00, 1.0000e+00, 4.8236e-01, -3.5763e-07,
-4.1421e-01, -7.3205e-01, -9.3185e-01, -1.0000e+00, -9.3185e-01,
-7.3205e-01, -4.1421e-01, 4.7684e-07, 4.8236e-01, 1.0000e+00],
grad_fn=<AddBackward0>)
最後,讓我們計算一個單元素輸出。當你對沒有引數的張量呼叫 `.backward()` 時,它期望呼叫張量只包含一個元素,就像計算損失函式時一樣。
tensor(25., grad_fn=<SumBackward0>)
我們張量中儲存的每個 `grad_fn` 都允許你透過其 `next_functions` 屬性將計算完全回溯到其輸入。我們可以在下面看到,透過此屬性深入 `d` 可以顯示所有先前張量的梯度函式。請注意,`a.grad_fn` 被報告為 `None`,這表明它是函式的輸入,沒有自己的歷史記錄。
print('d:')
print(d.grad_fn)
print(d.grad_fn.next_functions)
print(d.grad_fn.next_functions[0][0].next_functions)
print(d.grad_fn.next_functions[0][0].next_functions[0][0].next_functions)
print(d.grad_fn.next_functions[0][0].next_functions[0][0].next_functions[0][0].next_functions)
print('\nc:')
print(c.grad_fn)
print('\nb:')
print(b.grad_fn)
print('\na:')
print(a.grad_fn)
d:
<AddBackward0 object at 0x7f497c1b9ae0>
((<MulBackward0 object at 0x7f49741dc610>, 0), (None, 0))
((<SinBackward0 object at 0x7f49741dc610>, 0), (None, 0))
((<AccumulateGrad object at 0x7f497c1b9ae0>, 0),)
()
c:
<MulBackward0 object at 0x7f49741dc610>
b:
<SinBackward0 object at 0x7f49741dc610>
a:
None
有了所有這些機制,我們如何獲得導數?你呼叫輸出上的 `backward()` 方法,並檢查輸入的 `grad` 屬性來檢查梯度
out.backward()
print(a.grad)
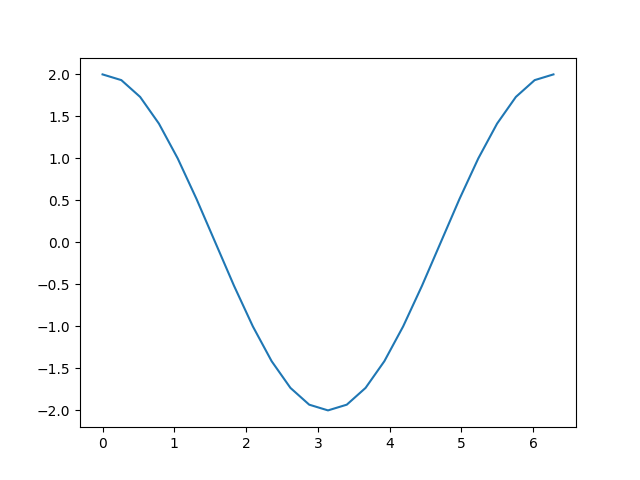
plt.plot(a.detach(), a.grad.detach())
tensor([ 2.0000e+00, 1.9319e+00, 1.7321e+00, 1.4142e+00, 1.0000e+00,
5.1764e-01, -8.7423e-08, -5.1764e-01, -1.0000e+00, -1.4142e+00,
-1.7321e+00, -1.9319e+00, -2.0000e+00, -1.9319e+00, -1.7321e+00,
-1.4142e+00, -1.0000e+00, -5.1764e-01, 2.3850e-08, 5.1764e-01,
1.0000e+00, 1.4142e+00, 1.7321e+00, 1.9319e+00, 2.0000e+00])
[<matplotlib.lines.Line2D object at 0x7f49b4dec4c0>]
回想一下我們為得到這裡所採取的計算步驟
新增一個常量,就像我們計算 `d` 時所做的一樣,不會改變導數。這就剩下 \(c = 2 * b = 2 * \sin(a)\),其導數應該是 \(2 * \cos(a)\)。檢視上面的圖,這正是我們看到的。
請注意,只有計算的*葉子節點*才計算其梯度。例如,如果你嘗試 `print(c.grad)`,你將得到 `None`。在這個簡單的例子中,只有輸入是葉子節點,因此只有它計算了梯度。
訓練中的 Autograd#
我們簡要了解了 autograd 的工作原理,但它在其預期用途中看起來是什麼樣的?讓我們定義一個小型模型並檢查它在單個訓練批次後的變化。首先,定義一些常量、我們的模型以及輸入和輸出的一些佔位符
BATCH_SIZE = 16
DIM_IN = 1000
HIDDEN_SIZE = 100
DIM_OUT = 10
class TinyModel(torch.nn.Module):
def __init__(self):
super(TinyModel, self).__init__()
self.layer1 = torch.nn.Linear(DIM_IN, HIDDEN_SIZE)
self.relu = torch.nn.ReLU()
self.layer2 = torch.nn.Linear(HIDDEN_SIZE, DIM_OUT)
def forward(self, x):
x = self.layer1(x)
x = self.relu(x)
x = self.layer2(x)
return x
some_input = torch.randn(BATCH_SIZE, DIM_IN, requires_grad=False)
ideal_output = torch.randn(BATCH_SIZE, DIM_OUT, requires_grad=False)
model = TinyModel()
你可能會注意到的一件事是我們從未為模型的層指定 `requires_grad=True`。在 `torch.nn.Module` 的子類中,我們假設我們想要跟蹤層權重的梯度以用於學習。
如果我們檢視模型的層,我們可以檢查權值的值,並驗證尚未計算任何梯度
print(model.layer2.weight[0][0:10]) # just a small slice
print(model.layer2.weight.grad)
tensor([ 0.0328, -0.0364, -0.0408, -0.0376, 0.0818, 0.0147, -0.0665, 0.0056,
-0.0273, -0.0751], grad_fn=<SliceBackward0>)
None
讓我們看看當我們在一個訓練批次中執行時會發生什麼。對於損失函式,我們將使用我們 `prediction` 和 `ideal_output` 之間的歐幾里得距離的平方,並且我們將使用一個基本的隨機梯度下降最佳化器。
optimizer = torch.optim.SGD(model.parameters(), lr=0.001)
prediction = model(some_input)
loss = (ideal_output - prediction).pow(2).sum()
print(loss)
tensor(157.6906, grad_fn=<SumBackward0>)
現在,讓我們呼叫 `loss.backward()` 看看會發生什麼
loss.backward()
print(model.layer2.weight[0][0:10])
print(model.layer2.weight.grad[0][0:10])
tensor([ 0.0328, -0.0364, -0.0408, -0.0376, 0.0818, 0.0147, -0.0665, 0.0056,
-0.0273, -0.0751], grad_fn=<SliceBackward0>)
tensor([ -3.3823, -5.1896, -10.4124, -6.9933, -4.6069, -2.6109, -0.1184,
-3.4189, -3.9634, -1.2222])
我們可以看到每個學習權重的梯度都被計算出來了,但權重保持不變,因為我們還沒有執行最佳化器。最佳化器負責根據計算出的梯度更新模型權重。
optimizer.step()
print(model.layer2.weight[0][0:10])
print(model.layer2.weight.grad[0][0:10])
tensor([ 0.0361, -0.0312, -0.0304, -0.0306, 0.0864, 0.0173, -0.0663, 0.0090,
-0.0233, -0.0738], grad_fn=<SliceBackward0>)
tensor([ -3.3823, -5.1896, -10.4124, -6.9933, -4.6069, -2.6109, -0.1184,
-3.4189, -3.9634, -1.2222])
你應該會看到 `layer2` 的權重已更改。
關於這個過程的一個重要事項:呼叫 `optimizer.step()` 後,你需要呼叫 `optimizer.zero_grad()`,否則每次執行 `loss.backward()` 時,學習權重的梯度都會累積
print(model.layer2.weight.grad[0][0:10])
for i in range(0, 5):
prediction = model(some_input)
loss = (ideal_output - prediction).pow(2).sum()
loss.backward()
print(model.layer2.weight.grad[0][0:10])
optimizer.zero_grad(set_to_none=False)
print(model.layer2.weight.grad[0][0:10])
tensor([ -3.3823, -5.1896, -10.4124, -6.9933, -4.6069, -2.6109, -0.1184,
-3.4189, -3.9634, -1.2222])
tensor([ -7.5784, -15.7621, -31.9912, -17.6633, -14.4308, -14.5418, 9.5047,
-7.6611, -11.0979, -1.2838])
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
執行上面的單元格後,你應該會看到,在多次執行 `loss.backward()` 後,大多數梯度的幅度會大得多。在執行下一個訓練批次之前未能清零梯度會導致梯度以這種方式爆炸,導致不正確和不可預測的學習結果。
關閉和開啟 Autograd#
在某些情況下,你需要精細控制 autograd 是否啟用。根據情況,有多種方法可以做到這一點。
最簡單的方法是直接更改張量上的 `requires_grad` 標誌
tensor([[1., 1., 1.],
[1., 1., 1.]], requires_grad=True)
tensor([[2., 2., 2.],
[2., 2., 2.]], grad_fn=<MulBackward0>)
tensor([[2., 2., 2.],
[2., 2., 2.]])
在上面的單元格中,我們看到 `b1` 有一個 `grad_fn`(即,一個被追蹤的計算歷史),這符合我們的預期,因為它源自一個具有 autograd 開啟的張量 `a`。當我們顯式使用 `a.requires_grad = False` 關閉 autograd 時,計算歷史不再被追蹤,正如我們在計算 `b2` 時所看到的。
如果你只需要臨時關閉 autograd,一個更好的方法是使用 `torch.no_grad()`
tensor([[5., 5., 5.],
[5., 5., 5.]], grad_fn=<AddBackward0>)
tensor([[5., 5., 5.],
[5., 5., 5.]])
tensor([[6., 6., 6.],
[6., 6., 6.]], grad_fn=<MulBackward0>)
`torch.no_grad()` 也可以用作函式或方法裝飾器
tensor([[5., 5., 5.],
[5., 5., 5.]], grad_fn=<AddBackward0>)
tensor([[5., 5., 5.],
[5., 5., 5.]])
有一個相應的上下文管理器 `torch.enable_grad()`,用於在 autograd 未啟用時將其啟用。它也可以用作裝飾器。
最後,你可能有一個需要梯度追蹤的張量,但你想要一個不需要它的副本。為此,我們有 `Tensor` 物件的 `detach()` 方法 - 它建立一個張量的副本,該副本*從*計算歷史中分離出來
tensor([0.9486, 0.8612, 0.2239, 0.8685, 0.9611], requires_grad=True)
tensor([0.9486, 0.8612, 0.2239, 0.8685, 0.9611])
我們上面這樣做是因為我們想繪製一些張量。這是因為 `matplotlib` 需要 NumPy 陣列作為輸入,而 PyTorch 張量到 NumPy 陣列的隱式轉換對於 `requires_grad=True` 的張量不啟用。製作一個分離的副本可以讓我們繼續前進。
Autograd 和就地操作#
在本筆記本中的所有示例中,我們都使用了變數來捕獲計算的中間值。Autograd 需要這些中間值來執行梯度計算。*因此,在使用 autograd 時,你必須小心使用就地操作。* 這樣做會破壞你在 `backward()` 呼叫中計算導數所需的資訊。PyTorch 甚至會阻止你嘗試對需要 autograd 的葉子變數進行就地操作,如下所示。
注意
以下程式碼單元格將引發執行時錯誤。這是預料之中的。
a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
torch.sin_(a)
Autograd Profiler#
Autograd 會詳細追蹤你計算的每一步。這樣的計算歷史,加上時間資訊,將成為一個有用的分析器 - 而 autograd 具有內建的此功能。這是一個簡單的用法示例
device = torch.device('cpu')
run_on_gpu = False
if torch.cuda.is_available():
device = torch.device('cuda')
run_on_gpu = True
x = torch.randn(2, 3, requires_grad=True)
y = torch.rand(2, 3, requires_grad=True)
z = torch.ones(2, 3, requires_grad=True)
with torch.autograd.profiler.profile(use_cuda=run_on_gpu) as prf:
for _ in range(1000):
z = (z / x) * y
print(prf.key_averages().table(sort_by='self_cpu_time_total'))
/var/lib/workspace/beginner_source/introyt/autogradyt_tutorial.py:485: FutureWarning:
The attribute `use_cuda` will be deprecated soon, please use ``use_device = 'cuda'`` instead.
------------------------------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------
Name Self CPU % Self CPU CPU total % CPU total CPU time avg Self CUDA Self CUDA % CUDA total CUDA time avg # of Calls
------------------------------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------
cudaEventRecord 43.09% 8.380ms 43.09% 8.380ms 2.095us 0.000us 0.00% 0.000us 0.000us 4000
aten::div 23.90% 4.649ms 23.90% 4.649ms 4.649us 8.455ms 50.02% 8.455ms 8.455us 1000
aten::mul 23.66% 4.601ms 23.66% 4.601ms 4.601us 8.448ms 49.98% 8.448ms 8.448us 1000
cudaGetDeviceProperties_v2 9.24% 1.797ms 9.24% 1.797ms 1.797ms 0.000us 0.00% 0.000us 0.000us 1
cudaDeviceSynchronize 0.09% 17.910us 0.09% 17.910us 17.910us 0.000us 0.00% 0.000us 0.000us 1
cudaDeviceGetStreamPriorityRange 0.01% 2.880us 0.01% 2.880us 2.880us 0.000us 0.00% 0.000us 0.000us 1
cudaStreamIsCapturing 0.01% 2.300us 0.01% 2.300us 0.767us 0.000us 0.00% 0.000us 0.000us 3
cudaGetDeviceCount 0.00% 0.380us 0.00% 0.380us 0.190us 0.000us 0.00% 0.000us 0.000us 2
------------------------------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------
Self CPU time total: 19.450ms
Self CUDA time total: 16.903ms
分析器還可以標記程式碼的各個子塊,按輸入張量形狀分解資料,並將資料匯出為 Chrome 跟蹤工具檔案。有關 API 的完整詳細資訊,請參閱*文件*。
高階主題:更多 Autograd 細節和高階 API#
如果你有一個具有 n 維輸入和 m 維輸出的函式 \(\vec{y}=f(\vec{x})\),那麼完整的梯度是一個關於每個輸入的所有輸出的導數的矩陣,稱為*雅可比矩陣*:
如果你有一個第二個函式,\(l=g\left(\vec{y}\right)\),它接受 m 維輸入(即,與上述輸出相同的維度),並返回一個標量輸出,你可以將其關於 \(\vec{y}\) 的梯度表示為一個列向量,\(v=\left(\begin{array}{ccc}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)^{T}\) - 這實際上只是一個單列的雅可比矩陣。
更具體地說,將第一個函式想象成你的 PyTorch 模型(可能有很多輸入和很多輸出),將第二個函式想象成一個損失函式(以模型輸出為輸入,以損失值為標量輸出)。
如果我們乘以第一個函式的雅可比矩陣和第二個函式的梯度,並應用鏈式法則,我們會得到
注意:你也可以使用等效操作 \(v^{T}\cdot J\),得到一個行向量。
所得的列向量是*第二個函式關於第一個函式輸入的梯度* - 或者在我們的模型和損失函式的情況下,是損失關於模型輸入的梯度。
``torch.autograd`` 是計算這些乘積的引擎。這就是我們在反向傳播過程中累積學習權重的梯度的方式。
因此,`backward()` 呼叫*也可以*接受一個可選的向量輸入。這個向量代表張量上的一組梯度,這些梯度被乘以其前面的 autograd 追蹤張量的雅可比矩陣。讓我們用一個小向量進行一個具體的例子
x = torch.randn(3, requires_grad=True)
y = x * 2
while y.data.norm() < 1000:
y = y * 2
print(y)
tensor([-1154.6906, -812.0412, 11.2324], grad_fn=<MulBackward0>)
如果我們現在嘗試呼叫 `y.backward()`,我們會收到一個執行時錯誤,並提示梯度只能*隱式*地為標量輸出計算。對於多維輸出,autograd 期望我們提供它可以乘以雅可比矩陣的三個輸出的梯度
v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float) # stand-in for gradients
y.backward(v)
print(x.grad)
tensor([5.1200e+01, 5.1200e+02, 5.1200e-02])
(請注意,輸出梯度都與二次冪有關 - 這是我們從重複加倍操作中期望的。)
高階 API#
autograd 上有一個 API,可以讓你直接訪問重要的微分矩陣和向量運算。特別是,它允許你計算特定函式在特定輸入下的雅可比矩陣和*海森矩陣*。(海森矩陣類似於雅可比矩陣,但表示所有*二階*偏導數。)它還提供了將向量與這些矩陣相乘的方法。
讓我們計算一個簡單函式在 2 個單元素輸入下的雅可比矩陣,並進行求值
def exp_adder(x, y):
return 2 * x.exp() + 3 * y
inputs = (torch.rand(1), torch.rand(1)) # arguments for the function
print(inputs)
torch.autograd.functional.jacobian(exp_adder, inputs)
(tensor([0.8778]), tensor([0.1108]))
(tensor([[4.8110]]), tensor([[3.]]))
如果你仔細觀察,第一個輸出應該等於 \(2e^x\)(因為 \(e^x\) 的導數是 \(e^x\)),第二個值應該是 3。
當然,你也可以對高階張量執行此操作
inputs = (torch.rand(3), torch.rand(3)) # arguments for the function
print(inputs)
torch.autograd.functional.jacobian(exp_adder, inputs)
(tensor([0.4431, 0.5910, 0.4504]), tensor([0.1194, 0.7245, 0.9486]))
(tensor([[3.1150, 0.0000, 0.0000],
[0.0000, 3.6115, 0.0000],
[0.0000, 0.0000, 3.1379]]), tensor([[3., 0., 0.],
[0., 3., 0.],
[0., 0., 3.]]))
假設你的函式是兩次可微的,`torch.autograd.functional.hessian()` 方法的工作方式相同,但返回一個包含所有二階導數的矩陣。
還有一個函式可以直接計算向量-雅可比矩陣乘積,如果你提供向量
def do_some_doubling(x):
y = x * 2
while y.data.norm() < 1000:
y = y * 2
return y
inputs = torch.randn(3)
my_gradients = torch.tensor([0.1, 1.0, 0.0001])
torch.autograd.functional.vjp(do_some_doubling, inputs, v=my_gradients)
(tensor([ 14.2352, 1376.1854, 264.1120]), tensor([2.0480e+02, 2.0480e+03, 2.0480e-01]))
`torch.autograd.functional.jvp()` 方法執行與 `vjp()` 相同的矩陣乘法,但運算元相反。`vhp()` 和 `hvp()` 方法對向量-海森乘積執行相同的操作。
有關更多資訊,包括*功能 API*的文件中的效能說明
指令碼總執行時間: (0 分鐘 0.828 秒)
