


注意
轉到末尾 下載完整的示例程式碼。
視覺化梯度#
作者: Justin Silver
本教程解釋瞭如何在神經網路的任何層提取和視覺化梯度。透過檢查資訊如何從網路末端流向我們想要最佳化的引數,我們可以除錯訓練過程中出現的梯度消失或爆炸等問題。
開始之前,請確保您理解張量及其操作方法。對autograd 的工作原理有基本瞭解也會很有幫助。
設定#
首先,請確保已安裝 PyTorch,然後匯入必要的庫。
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import matplotlib.pyplot as plt
接下來,我們將建立一個用於 MNIST 資料集的網路,其架構類似於批次歸一化論文中描述的。
為了說明梯度視覺化的重要性,我們將例項化一個帶有批次歸一化 (BatchNorm) 的網路版本和一個不帶批次歸一化的版本。批次歸一化是一種非常有效的解決梯度消失/爆炸的技術,我們將透過實驗來驗證這一點。
我們使用的模型具有可配置數量的重複全連線層,這些層在 nn.Linear、norm_layer 和 nn.Sigmoid 之間交替。如果啟用了批次歸一化,則 norm_layer 將使用 BatchNorm1d,否則將使用 Identity 變換。
def fc_layer(in_size, out_size, norm_layer):
"""Return a stack of linear->norm->sigmoid layers"""
return nn.Sequential(nn.Linear(in_size, out_size), norm_layer(out_size), nn.Sigmoid())
class Net(nn.Module):
"""Define a network that has num_layers of linear->norm->sigmoid transformations"""
def __init__(self, in_size=28*28, hidden_size=128,
out_size=10, num_layers=3, batchnorm=False):
super().__init__()
if batchnorm is False:
norm_layer = nn.Identity
else:
norm_layer = nn.BatchNorm1d
layers = []
layers.append(fc_layer(in_size, hidden_size, norm_layer))
for i in range(num_layers-1):
layers.append(fc_layer(hidden_size, hidden_size, norm_layer))
layers.append(nn.Linear(hidden_size, out_size))
self.layers = nn.Sequential(*layers)
def forward(self, x):
x = torch.flatten(x, 1)
return self.layers(x)
接下來,我們設定一些模擬資料,例項化兩個模型版本,並初始化最佳化器。
# set up dummy data
x = torch.randn(10, 28, 28)
y = torch.randint(10, (10, ))
# init model
model_bn = Net(batchnorm=True, num_layers=3)
model_nobn = Net(batchnorm=False, num_layers=3)
model_bn.train()
model_nobn.train()
optimizer_bn = optim.SGD(model_bn.parameters(), lr=0.01, momentum=0.9)
optimizer_nobn = optim.SGD(model_nobn.parameters(), lr=0.01, momentum=0.9)
我們可以透過探測其中一個內部層來驗證批次歸一化僅應用於其中一個模型。
print(model_bn.layers[0])
print(model_nobn.layers[0])
Sequential(
(0): Linear(in_features=784, out_features=128, bias=True)
(1): BatchNorm1d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): Sigmoid()
)
Sequential(
(0): Linear(in_features=784, out_features=128, bias=True)
(1): Identity()
(2): Sigmoid()
)
註冊鉤子#
由於我們將模型的邏輯和狀態封裝在 nn.Module 中,如果我們想避免直接修改模組程式碼,就需要另一種方法來訪問中間梯度。這可以透過註冊鉤子來完成。
警告
與在張量本身上使用 retain_grad() 相比,更推薦使用附加在輸出張量上的反向傳播鉤子。另一種方法是直接附加模組鉤子(例如 register_full_backward_hook()),只要 nn.Module 例項不執行任何就地操作。有關更多資訊,請參閱此 issue。
以下程式碼定義了我們的鉤子,併為網路的層收集了描述性名稱。
# note that wrapper functions are used for Python closure
# so that we can pass arguments.
def hook_forward(module_name, grads, hook_backward):
def hook(module, args, output):
"""Forward pass hook which attaches backward pass hooks to intermediate tensors"""
output.register_hook(hook_backward(module_name, grads))
return hook
def hook_backward(module_name, grads):
def hook(grad):
"""Backward pass hook which appends gradients"""
grads.append((module_name, grad))
return hook
def get_all_layers(model, hook_forward, hook_backward):
"""Register forward pass hook (which registers a backward hook) to model outputs
Returns:
- layers: a dict with keys as layer/module and values as layer/module names
e.g. layers[nn.Conv2d] = layer1.0.conv1
- grads: a list of tuples with module name and tensor output gradient
e.g. grads[0] == (layer1.0.conv1, tensor.Torch(...))
"""
layers = dict()
grads = []
for name, layer in model.named_modules():
# skip Sequential and/or wrapper modules
if any(layer.children()) is False:
layers[layer] = name
layer.register_forward_hook(hook_forward(name, grads, hook_backward))
return layers, grads
# register hooks
layers_bn, grads_bn = get_all_layers(model_bn, hook_forward, hook_backward)
layers_nobn, grads_nobn = get_all_layers(model_nobn, hook_forward, hook_backward)
訓練與視覺化#
現在,讓我們訓練模型幾個 epoch。
epochs = 10
for epoch in range(epochs):
# important to clear, because we append to
# outputs everytime we do a forward pass
grads_bn.clear()
grads_nobn.clear()
optimizer_bn.zero_grad()
optimizer_nobn.zero_grad()
y_pred_bn = model_bn(x)
y_pred_nobn = model_nobn(x)
loss_bn = F.cross_entropy(y_pred_bn, y)
loss_nobn = F.cross_entropy(y_pred_nobn, y)
loss_bn.backward()
loss_nobn.backward()
optimizer_bn.step()
optimizer_nobn.step()
執行前向和反向傳播後,所有中間張量的梯度應該都存在於 grads_bn 和 grads_nobn 中。我們計算每個梯度矩陣的平均絕對值,以便比較這兩個模型。
def get_grads(grads):
layer_idx = []
avg_grads = []
for idx, (name, grad) in enumerate(grads):
if grad is not None:
avg_grad = grad.abs().mean()
avg_grads.append(avg_grad)
# idx is backwards since we appended in backward pass
layer_idx.append(len(grads) - 1 - idx)
return layer_idx, avg_grads
layer_idx_bn, avg_grads_bn = get_grads(grads_bn)
layer_idx_nobn, avg_grads_nobn = get_grads(grads_nobn)
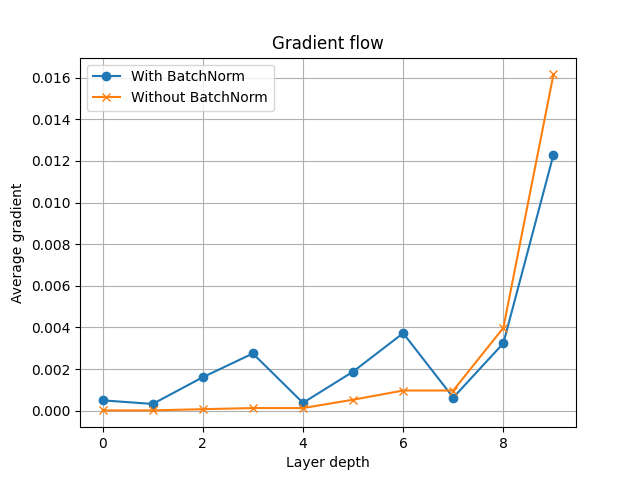
計算了平均梯度後,我們現在可以繪製它們,並檢視值隨網路深度的變化。請注意,當我們不應用批次歸一化時,中間層的梯度值會很快變為零。然而,批次歸一化模型在其中間層保持非零梯度。
fig, ax = plt.subplots()
ax.plot(layer_idx_bn, avg_grads_bn, label="With BatchNorm", marker="o")
ax.plot(layer_idx_nobn, avg_grads_nobn, label="Without BatchNorm", marker="x")
ax.set_xlabel("Layer depth")
ax.set_ylabel("Average gradient")
ax.set_title("Gradient flow")
ax.grid(True)
ax.legend()
plt.show()
結論#
在本教程中,我們演示瞭如何視覺化封裝在 nn.Module 類中的神經網路的梯度流。我們定性地展示了批次歸一化如何幫助緩解深度神經網路中出現的梯度消失問題。
如果您想了解更多關於 PyTorch 的 autograd 系統如何工作的資訊,請訪問下面的參考文獻。如果您對此教程有任何反饋(改進、拼寫錯誤等),請使用PyTorch 論壇和/或issue tracker與我們聯絡。
(可選) 附加練習#
嘗試增加模型中層的數量(
num_layers),看看這對梯度流圖有什麼影響。如何修改程式碼來視覺化平均啟用而不是平均梯度?(*提示:在 hook_forward() 函式中,我們可以訪問原始張量輸出*)
還有哪些其他方法可以處理梯度消失和爆炸問題?
參考文獻#
指令碼總執行時間: (0 分鐘 0.288 秒)
