評價此頁
★ ★ ★ ★ ★
torch.autograd">
beginner/basics/autogradqs_tutorial

注意

前往底部 下載完整示例程式碼。

學習基礎知識 || 快速入門 || 張量 || 資料集 & DataLoader || Transforms || 構建模型 || 自動微分 || 最佳化 || 儲存 & 載入模型

使用 torch.autograd 進行自動微分#

建立時間：2021年2月10日 | 最後更新：2024年1月16日 | 最後驗證：2024年11月5日

在訓練神經網路時，最常用的演算法是反向傳播。在該演算法中，引數（模型權重）會根據損失函式相對於給定引數的梯度進行調整。

為了計算這些梯度，PyTorch 擁有一個內建的微分引擎，稱為 torch.autograd。它支援對任何計算圖進行自動梯度計算。

考慮最簡單的單層神經網路，它具有輸入 x、引數 w 和 b，以及某個損失函式。它可以用 PyTorch 以以下方式定義：

import torch

x = torch.ones(5)  # input tensor
y = torch.zeros(3)  # expected output
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

張量、函式和計算圖#

此程式碼定義了以下計算圖：

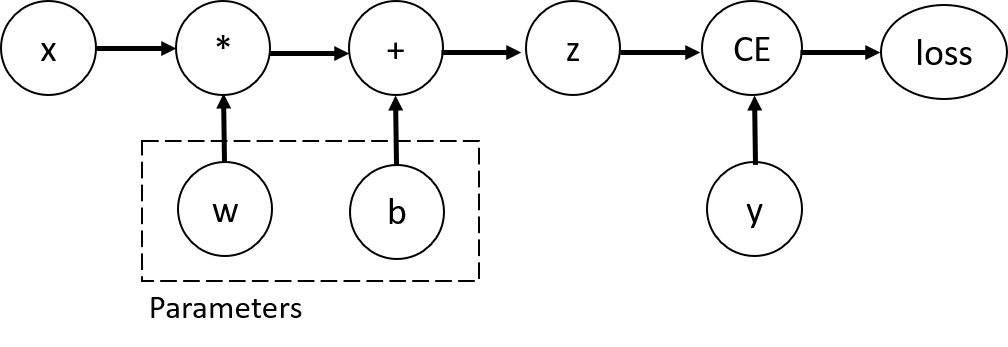
在此網路中，w 和 b 是引數，我們需要對它們進行最佳化。因此，我們需要能夠計算損失函式相對於這些變數的梯度。為了做到這一點，我們將這些張量的 requires_grad 屬性設定為 True。

注意

您可以在建立張量時設定 requires_grad 的值，或者稍後透過使用 x.requires_grad_(True) 方法來設定。

我們將用於構建計算圖的函式實際上是 Function 類的一個物件。該物件知道如何在前向計算函式，也知道如何在反向傳播步驟中計算其導數。反向傳播函式的引用儲存在張量的 grad_fn 屬性中。您可以在文件中找到有關 Function 的更多資訊。

print(f"Gradient function for z = {z.grad_fn}")
print(f"Gradient function for loss = {loss.grad_fn}")

Gradient function for z = <AddBackward0 object at 0x7f5e21259ff0>
Gradient function for loss = <BinaryCrossEntropyWithLogitsBackward0 object at 0x7f5e2125ad10>

計算梯度#

要最佳化神經網路中引數的權重，我們需要計算損失函式相對於引數的導數，即，在 x 和 y 的某些固定值下，我們需要得到 \(\frac{\partial loss}{\partial w}\) 和 \(\frac{\partial loss}{\partial b}\)。為了計算這些導數，我們呼叫 loss.backward()，然後從 w.grad 和 b.grad 中檢索值。

loss.backward()
print(w.grad)
print(b.grad)

tensor([[0.0082, 0.2994, 0.0587],
        [0.0082, 0.2994, 0.0587],
        [0.0082, 0.2994, 0.0587],
        [0.0082, 0.2994, 0.0587],
        [0.0082, 0.2994, 0.0587]])
tensor([0.0082, 0.2994, 0.0587])

注意

  • 我們只能獲取計算圖葉子節點（其 requires_grad 屬性設定為 True）的 grad 屬性。對於我們圖中的所有其他節點，梯度將不可用。

  • 出於效能原因，我們只能對給定的圖執行一次梯度計算（呼叫 backward）。如果我們需要在同一圖上進行多次 backward 呼叫，我們需要將 retain_graph=True 傳遞給 backward 呼叫。

停用梯度跟蹤#

預設情況下，所有 requires_grad=True 的張量都會跟蹤它們的計算歷史並支援梯度計算。但是，在某些情況下我們不需要這樣做，例如，當我們訓練好模型並只想將其應用於某些輸入資料時，即我們只想透過網路進行前向計算。我們可以將計算程式碼用 torch.no_grad() 塊包圍來停止跟蹤計算。

z = torch.matmul(x, w)+b
print(z.requires_grad)

with torch.no_grad():
    z = torch.matmul(x, w)+b
print(z.requires_grad)

True
False

另一種實現相同結果的方法是使用張量的 detach() 方法。

z = torch.matmul(x, w)+b
z_det = z.detach()
print(z_det.requires_grad)

False
有理由停用梯度跟蹤：

  • 將神經網路中的某些引數標記為凍結引數。

  • 在只進行前向傳播時加速計算，因為對不跟蹤梯度的張量進行計算會更有效。

關於計算圖的更多資訊#

從概念上講，autograd 在一個由 Function 物件組成的有向無環圖 (DAG) 中，會記錄資料（張量）和所有執行的操作（以及由此產生的新張量）。在這個 DAG 中，葉子是輸入張量，根是輸出張量。透過從根到葉追蹤這個圖，您可以使用鏈式法則自動計算梯度。

在前向傳播中，autograd 同時執行兩項操作：

  • 執行請求的操作以計算結果張量

  • 在 DAG 中維護該操作的梯度函式。

當在 DAG 根上呼叫 .backward() 時，反向傳播開始。此時，autograd 會

  • 從每個 .grad_fn 計算梯度，

  • 將它們累積到相應張量的 .grad 屬性中，

  • 使用鏈式法則，一直傳播到葉子張量。

注意

PyTorch 中的 DAG 是動態的 一個重要的注意事項是圖是從頭開始重新建立的；每次呼叫 .backward() 後，autograd 都會開始填充一個新圖。這正是允許您在模型中使用控制流語句的原因；您可以根據需要更改每個迭代的形狀、大小和操作。

可選閱讀：張量梯度和雅可比乘積#

在許多情況下，我們有一個標量損失函式，我們需要計算相對於某些引數的梯度。然而，在某些情況下，輸出函式是一個任意張量。在這種情況下，PyTorch 允許您計算所謂的雅可比乘積，而不是實際的梯度。

對於向量函式 \(\vec{y}=f(\vec{x})\)，其中 \(\vec{x}=\langle x_1,\dots,x_n\rangle\) 和 \(\vec{y}=\langle y_1,\dots,y_m\rangle\)，\(\vec{y}\) 相對於 \(\vec{x}\) 的梯度由雅可比矩陣給出：

\[J=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\]

PyTorch 允許您為給定的輸入向量 \(v=(v_1 \dots v_m)\) 計算雅可比乘積 \(v^T\cdot J\)，而不是計算雅可比矩陣本身。這是透過將 \(v\) 作為引數傳遞給 backward 來實現的。 \(v\) 的大小應與我們想要計算乘積的原始張量的大小相同。

inp = torch.eye(4, 5, requires_grad=True)
out = (inp+1).pow(2).t()
out.backward(torch.ones_like(out), retain_graph=True)
print(f"First call\n{inp.grad}")
out.backward(torch.ones_like(out), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(out), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")

First call
tensor([[4., 2., 2., 2., 2.],
        [2., 4., 2., 2., 2.],
        [2., 2., 4., 2., 2.],
        [2., 2., 2., 4., 2.]])

Second call
tensor([[8., 4., 4., 4., 4.],
        [4., 8., 4., 4., 4.],
        [4., 4., 8., 4., 4.],
        [4., 4., 4., 8., 4.]])

Call after zeroing gradients
tensor([[4., 2., 2., 2., 2.],
        [2., 4., 2., 2., 2.],
        [2., 2., 4., 2., 2.],
        [2., 2., 2., 4., 2.]])

請注意，當我們使用相同的引數第二次呼叫 backward 時，梯度值是不同的。發生這種情況是因為在進行 backward 傳播時，PyTorch 會累積梯度，也就是說，計算出的梯度值會被加到計算圖所有葉子節點的 grad 屬性上。如果您想計算正確的梯度，您需要先將 grad 屬性歸零。在實際訓練中，最佳化器會幫助我們做到這一點。

注意

之前我們呼叫了不帶引數的 backward() 函式。這本質上等同於呼叫 backward(torch.tensor(1.0))，這在神經網路訓練等標量值函式的情況下，是計算梯度的有用方法。

進一步閱讀#

指令碼總執行時間： (0 分鐘 0.146 秒)

在此頁面上
PyTorch 庫