beginner/fgsm_tutorial

在 Google Colab 中執行

Colab

下載 Notebook

Notebook

在 GitHub 上檢視

GitHub

對抗樣本生成

建立時間：2018年8月14日 | 最後更新：2025年1月27日 | 最後驗證：未驗證

作者： Nathan Inkawhich

如果您正在閱讀本文，希望您能認識到一些機器學習模型的有效性。研究不斷推動著機器學習模型變得更快、更準確、更高效。然而，在設計和訓練模型時，一個常常被忽視的方面是安全性和魯棒性，尤其是在面對希望愚弄模型的對手時。

本教程將提高您對機器學習模型安全漏洞的認識，並深入探討對抗性機器學習這一熱門話題。您可能會驚訝地發現，向影像新增不易察覺的微小擾動會導致模型效能發生巨大差異。鑑於這是一篇教程，我們將透過一個影像分類器的示例來探討這個話題。具體來說，我們將使用最早也是最受歡迎的攻擊方法之一——快速梯度符號攻擊 (FGSM) 來愚弄一個 MNIST 分類器。

威脅模型

為了提供背景資訊，存在許多類別的對抗性攻擊，每種攻擊都有不同的目標和對攻擊者知識的假設。然而，總的來說，其總體目標是以最小的擾動修改輸入資料以導致期望的錯誤分類。攻擊者的知識存在幾種假設，其中兩種是：白盒攻擊和黑盒攻擊。白盒攻擊假設攻擊者對模型擁有完全的知識和訪問許可權，包括架構、輸入、輸出和權重。黑盒攻擊假設攻擊者只能訪問模型的輸入和輸出，而對底層架構或權重一無所知。目標也有幾種型別，包括誤分類和源/目標誤分類。誤分類的目標意味著攻擊者只希望輸出分類錯誤，而不關心新的分類是什麼。源/目標誤分類意味著攻擊者希望修改一個最初屬於特定源類別的影像，使其被分類為特定的目標類別。

在這種情況下，FGSM 攻擊是一種以誤分類為目標的白盒攻擊。有了這些背景資訊，我們現在可以詳細討論該攻擊。

快速梯度符號攻擊

目前最早也是最受歡迎的對抗性攻擊之一被稱為快速梯度符號攻擊 (FGSM)，由 Goodfellow 等人在 《解釋和利用對抗樣本》 中進行了描述。這種攻擊異常強大，卻又直觀。它利用神經網路的學習方式——梯度——來攻擊它們。思路很簡單，攻擊不是透過基於反向傳播的梯度調整權重來最小化損失，而是基於相同的反向傳播梯度，調整輸入資料以最大化損失。換句話說，攻擊使用損失關於輸入資料的梯度，然後調整輸入資料以最大化損失。

在開始編寫程式碼之前，讓我們看一下著名的 FGSM 熊貓示例，並提取一些符號。

從圖中可以看出，\(\mathbf{x}\) 是被正確分類為“熊貓”的原始輸入影像，\(y\) 是 \(\mathbf{x}\) 的真實標籤，\(\mathbf{\theta}\) 表示模型引數，而 \(\mathbf{J}(\mathbf{\theta}, \mathbf{x}, y)\) 是用於訓練網路的損失。攻擊將梯度反向傳播到輸入資料以計算 \(\nabla_{x} J(\mathbf{\theta}, \mathbf{x}, y)\)。然後，它沿最大化損失的方向（即 \(sign(\nabla_{x} J(\mathbf{\theta}, \mathbf{x}, y))\)）以一個小的步長（圖片中為 \(\epsilon\) 或 \(0.007\)）調整輸入資料。得到的擾動影像 \(x'\)，然後被目標網路誤分類為“長臂猿”，儘管它仍然明顯是“熊貓”。

希望現在本教程的動機已經很清楚了，那麼讓我們開始實現。

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt

實現

在本節中，我們將討論本教程的輸入引數，定義被攻擊的模型，然後編寫攻擊程式碼並執行一些測試。

輸入

本教程只有三個輸入，定義如下：

• epsilons - 用於執行的 epsilon 值列表。在列表中包含 0 很重要，因為它代表模型在原始測試集上的效能。此外，直觀上我們期望 epsilon 值越大，擾動越明顯，但攻擊在降低模型準確性方面越有效。由於這裡的資料範圍是 \([0,1]\)，任何 epsilon 值都不應超過 1。

• pretrained_model - 預訓練的 MNIST 模型路徑，該模型使用 pytorch/examples/mnist 進行訓練。為簡單起見，請在此處 下載 預訓練模型。

epsilons = [0, .05, .1, .15, .2, .25, .3]
pretrained_model = "data/lenet_mnist_model.pth"
# Set random seed for reproducibility
torch.manual_seed(42)

<torch._C.Generator object at 0x7fe4953749b0>

被攻擊的模型

如前所述，被攻擊的模型與 pytorch/examples/mnist 中的 MNIST 模型相同。您可以訓練並儲存自己的 MNIST 模型，也可以下載並使用提供的模型。這裡的Net定義和測試資料載入器是從 MNIST 示例中複製的。本節的目的是定義模型和資料載入器，然後初始化模型並載入預訓練權重。

# LeNet Model definition
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 32, 3, 1)
        self.conv2 = nn.Conv2d(32, 64, 3, 1)
        self.dropout1 = nn.Dropout(0.25)
        self.dropout2 = nn.Dropout(0.5)
        self.fc1 = nn.Linear(9216, 128)
        self.fc2 = nn.Linear(128, 10)

    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.conv2(x)
        x = F.relu(x)
        x = F.max_pool2d(x, 2)
        x = self.dropout1(x)
        x = torch.flatten(x, 1)
        x = self.fc1(x)
        x = F.relu(x)
        x = self.dropout2(x)
        x = self.fc2(x)
        output = F.log_softmax(x, dim=1)
        return output

# MNIST Test dataset and dataloader declaration
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, download=True, transform=transforms.Compose([
            transforms.ToTensor(),
            transforms.Normalize((0.1307,), (0.3081,)),
            ])),
        batch_size=1, shuffle=True)

# We want to be able to train our model on an `accelerator <https://pytorch.com.tw/docs/stable/torch.html#accelerators>`__
# such as CUDA, MPS, MTIA, or XPU. If the current accelerator is available, we will use it. Otherwise, we use the CPU.
device = torch.accelerator.current_accelerator().type if torch.accelerator.is_available() else "cpu"
print(f"Using {device} device")

# Initialize the network
model = Net().to(device)

# Load the pretrained model
model.load_state_dict(torch.load(pretrained_model, map_location=device, weights_only=True))

# Set the model in evaluation mode. In this case this is for the Dropout layers
model.eval()

  0%|          | 0.00/9.91M [00:00<?, ?B/s]
100%|██████████| 9.91M/9.91M [00:00<00:00, 128MB/s]

  0%|          | 0.00/28.9k [00:00<?, ?B/s]
100%|██████████| 28.9k/28.9k [00:00<00:00, 31.9MB/s]

  0%|          | 0.00/1.65M [00:00<?, ?B/s]
100%|██████████| 1.65M/1.65M [00:00<00:00, 164MB/s]

  0%|          | 0.00/4.54k [00:00<?, ?B/s]
100%|██████████| 4.54k/4.54k [00:00<00:00, 27.4MB/s]
Using cuda device

Net(
  (conv1): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1))
  (conv2): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1))
  (dropout1): Dropout(p=0.25, inplace=False)
  (dropout2): Dropout(p=0.5, inplace=False)
  (fc1): Linear(in_features=9216, out_features=128, bias=True)
  (fc2): Linear(in_features=128, out_features=10, bias=True)
)

FGSM 攻擊

現在，我們可以定義透過擾動原始輸入來建立對抗樣本的函式。 fgsm_attack 函式接受三個輸入：image 是原始的乾淨影像 (\(x\))，epsilon 是畫素擾動量 (\(\epsilon\))，data_grad 是損失關於輸入影像的梯度 (\(\nabla_{x} J(\mathbf{\theta}, \mathbf{x}, y)\))。然後，該函式建立擾動影像，如下所示：

\[perturbed\_image = image + epsilon*sign(data\_grad) = x + \epsilon * sign(\nabla_{x} J(\mathbf{\theta}, \mathbf{x}, y)) \]

最後，為了保持資料的原始範圍，將擾動後的影像裁剪到 \([0,1]\) 範圍內。

# FGSM attack code
def fgsm_attack(image, epsilon, data_grad):
    # Collect the element-wise sign of the data gradient
    sign_data_grad = data_grad.sign()
    # Create the perturbed image by adjusting each pixel of the input image
    perturbed_image = image + epsilon*sign_data_grad
    # Adding clipping to maintain [0,1] range
    perturbed_image = torch.clamp(perturbed_image, 0, 1)
    # Return the perturbed image
    return perturbed_image

# restores the tensors to their original scale
def denorm(batch, mean=[0.1307], std=[0.3081]):
    """
    Convert a batch of tensors to their original scale.

    Args:
        batch (torch.Tensor): Batch of normalized tensors.
        mean (torch.Tensor or list): Mean used for normalization.
        std (torch.Tensor or list): Standard deviation used for normalization.

    Returns:
        torch.Tensor: batch of tensors without normalization applied to them.
    """
    if isinstance(mean, list):
        mean = torch.tensor(mean).to(device)
    if isinstance(std, list):
        std = torch.tensor(std).to(device)

    return batch * std.view(1, -1, 1, 1) + mean.view(1, -1, 1, 1)

測試函式

最後，本教程的核心結果來自 test 函式。每次呼叫此測試函式都會在 MNIST 測試集上執行完整的測試步驟並報告最終準確率。但是，請注意，此函式還接受一個epsilon輸入。這是因為 test 函式報告了在 \(\epsilon\) 強度下受到攻擊的模型的準確率。更具體地說，對於測試集中的每個樣本，該函式計算損失關於輸入資料的梯度（\(data\_grad\)），使用 fgsm_attack 建立擾動影像（\(perturbed\_data\)），然後檢查擾動後的樣本是否具有對抗性。除了測試模型的準確率外，該函式還儲存並返回一些成功的對抗樣本，以便稍後進行視覺化。

def test( model, device, test_loader, epsilon ):

    # Accuracy counter
    correct = 0
    adv_examples = []

    # Loop over all examples in test set
    for data, target in test_loader:

        # Send the data and label to the device
        data, target = data.to(device), target.to(device)

        # Set requires_grad attribute of tensor. Important for Attack
        data.requires_grad = True

        # Forward pass the data through the model
        output = model(data)
        init_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability

        # If the initial prediction is wrong, don't bother attacking, just move on
        if init_pred.item() != target.item():
            continue

        # Calculate the loss
        loss = F.nll_loss(output, target)

        # Zero all existing gradients
        model.zero_grad()

        # Calculate gradients of model in backward pass
        loss.backward()

        # Collect ``datagrad``
        data_grad = data.grad.data

        # Restore the data to its original scale
        data_denorm = denorm(data)

        # Call FGSM Attack
        perturbed_data = fgsm_attack(data_denorm, epsilon, data_grad)

        # Reapply normalization
        perturbed_data_normalized = transforms.Normalize((0.1307,), (0.3081,))(perturbed_data)

        # Re-classify the perturbed image
        output = model(perturbed_data_normalized)

        # Check for success
        final_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability
        if final_pred.item() == target.item():
            correct += 1
            # Special case for saving 0 epsilon examples
            if epsilon == 0 and len(adv_examples) < 5:
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
        else:
            # Save some adv examples for visualization later
            if len(adv_examples) < 5:
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )

    # Calculate final accuracy for this epsilon
    final_acc = correct/float(len(test_loader))
    print(f"Epsilon: {epsilon}\tTest Accuracy = {correct} / {len(test_loader)} = {final_acc}")

    # Return the accuracy and an adversarial example
    return final_acc, adv_examples

執行攻擊

實現部分的最後一步是實際執行攻擊。在這裡，我們對epsilons輸入中的每個 epsilon 值執行一個完整的測試步驟。對於每個 epsilon，我們還儲存最終的準確率和一些成功的對抗樣本，以便在接下來的部分進行繪製。請注意，隨著 epsilon 值的增加，打印出的準確率如何下降。另外，請注意 \(\epsilon=0\) 的情況代表原始測試準確率，沒有受到攻擊。

accuracies = []
examples = []

# Run test for each epsilon
for eps in epsilons:
    acc, ex = test(model, device, test_loader, eps)
    accuracies.append(acc)
    examples.append(ex)

Epsilon: 0      Test Accuracy = 9912 / 10000 = 0.9912
Epsilon: 0.05   Test Accuracy = 9605 / 10000 = 0.9605
Epsilon: 0.1    Test Accuracy = 8743 / 10000 = 0.8743
Epsilon: 0.15   Test Accuracy = 7108 / 10000 = 0.7108
Epsilon: 0.2    Test Accuracy = 4859 / 10000 = 0.4859
Epsilon: 0.25   Test Accuracy = 2718 / 10000 = 0.2718
Epsilon: 0.3    Test Accuracy = 1411 / 10000 = 0.1411

結果

準確率與 Epsilon 的關係

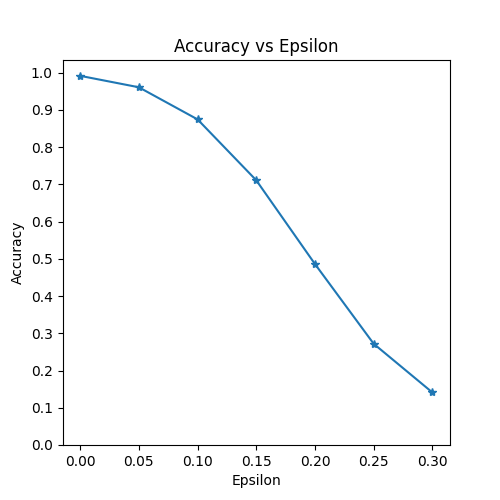
第一個結果是準確率與 epsilon 的關係圖。如前所述，隨著 epsilon 的增加，我們期望測試準確率下降。這是因為更大的 epsilon 意味著我們在最大化損失的方向上邁出更大的步子。請注意，儘管 epsilon 值是線性間隔的，但曲線的趨勢並非線性。例如，\(\epsilon=0.05\) 時的準確率僅比 \(\epsilon=0\) 時低約 4%，而 \(\epsilon=0.2\) 時的準確率比 \(\epsilon=0.15\) 時低 25%。另外，請注意，模型在 \(\epsilon=0.25\) 和 \(\epsilon=0.3\) 之間的準確率達到了 10 類分類器的隨機準確率。

plt.figure(figsize=(5,5))
plt.plot(epsilons, accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()

示例對抗樣本

還記得“天下沒有免費的午餐”嗎？在這種情況下，隨著 epsilon 的增加，測試準確率下降，但是擾動也更容易被察覺。實際上，在準確率下降和可感知性之間存在一個權衡，攻擊者必須考慮這一點。在這裡，我們展示了一些在每個 epsilon 值下的成功對抗樣本的例子。繪圖的每一行都顯示了一個不同的 epsilon 值。第一行是 \(\epsilon=0\) 的示例，代表沒有擾動的原始“乾淨”影像。每張影像的標題顯示“原始分類 -> 對抗性分類”。請注意，在 \(\epsilon=0.15\) 時，擾動開始變得明顯，而在 \(\epsilon=0.3\) 時則非常明顯。然而，在所有情況下，人類仍然能夠識別正確的類別，儘管添加了噪聲。

# Plot several examples of adversarial samples at each epsilon
cnt = 0
plt.figure(figsize=(8,10))
for i in range(len(epsilons)):
    for j in range(len(examples[i])):
        cnt += 1
        plt.subplot(len(epsilons),len(examples[0]),cnt)
        plt.xticks([], [])
        plt.yticks([], [])
        if j == 0:
            plt.ylabel(f"Eps: {epsilons[i]}", fontsize=14)
        orig,adv,ex = examples[i][j]
        plt.title(f"{orig} -> {adv}")
        plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()

下一步去哪兒？

希望本教程能讓您對對抗性機器學習這一主題有所瞭解。從這裡可以有很多潛在的方向。這種攻擊代表了對抗性攻擊研究的開端，此後出現了許多關於如何從攻擊者那裡攻擊和防禦機器學習模型的後續想法。事實上，在 NIPS 2017 上曾舉辦過一次對抗性攻擊和防禦競賽，競賽中使用的許多方法都在這篇論文中進行了描述：對抗性攻擊和防禦競賽。防禦工作也引出了使機器學習模型整體上更加魯棒的想法，無論是對自然擾動輸入還是對抗性精心設計的輸入。

另一個方向是不同領域的對抗性攻擊和防禦。對抗性研究不僅限於影像領域，請檢視 這項 對語音轉文字模型的攻擊。但或許瞭解對抗性機器學習的最好方法是親自動手實踐。嘗試實現 NIPS 2017 競賽中的另一種攻擊，看看它與 FGSM 有何不同。然後，嘗試從您自己的攻擊中防禦模型。

另一個方向，取決於可用資源，是修改程式碼以支援批處理、並行和/或分散式處理工作，而不是在上面的每個 epsilon test() 迴圈中一次處理一個攻擊。