稀疏性概述¶
稀疏性是一種從神經網路中移除引數的技術,以降低其記憶體開銷或延遲。透過仔細選擇剪枝元素的方式,可以在不顯著犧牲模型質量(準確率/f1值)的情況下,顯著降低記憶體開銷和延遲。
目標¶
我們認為當前稀疏性研究人員/使用者面臨的主要問題是碎片化。研究人員理應展示端到端的成果,但這卻意味著他們需要花費大量時間來弄清楚如何與 PyTorch 整合,以及實現上的問題,例如:
何時應該進行掩碼處理?
何時/如何儲存壓縮表示?
是否需要原地或非原地掩碼更新?
如何呼叫稀疏矩陣乘法而不是密集矩陣乘法?
我們認為上述問題可以透過 torchao 一次性解決,讓研究人員專注於真正重要的事情——提升稀疏核效能或更精確的剪枝演算法。
更具體地說,我們希望為稀疏核(張量子類)和剪枝演算法(torch.ao.pruning.Sparsifier)提供使用者可以擴充套件的教程和 API。我們的目標是提供模組化的構建塊,不僅可以用於加速推理,還可以用於訓練,並且可以很好地與 torchao 量化工作流結合使用。
從頭開始訓練稀疏模型,並實現硬體加速,同時將準確率損失降至最低。
使用自定義剪枝演算法恢復剪枝模型的準確率損失。
在支援稀疏性的硬體上加速掩碼/剪枝模型,以實現效能提升。
設計¶
稀疏性與量化一樣,是一種準確率/效能的權衡,我們不僅關心加速效果,還關心架構最佳化技術的準確率下降情況。
在量化中,理論效能增益通常由我們量化到的資料型別決定——從 float32 量化到 float16 會帶來理論上的 2 倍加速。對於剪枝/稀疏性,類似的變數將是稀疏級別/稀疏模式。對於半結構化稀疏性,稀疏級別固定為 50%,因此我們期望理論上能有 2 倍的提升。對於塊稀疏矩陣和非結構化稀疏性,加速效果是可變的,取決於張量的稀疏級別。
稀疏性和量化之間的一個關鍵區別在於準確率下降的確定方式:通常,量化的準確率下降由所選的 scale 和 zero_point 決定。然而,在剪枝中,準確率下降取決於掩碼。稀疏性和量化密切相關,並且共享量化/稀疏感知訓練等準確率緩解技術。
透過仔細選擇指定的元素並重新訓練網路,剪枝可以實現可忽略的準確率下降,甚至在某些情況下可以略微提高準確率。這是一個活躍的研究領域,目前尚未達成一致意見。我們期望使用者會根據自己設定的目標稀疏模式進行剪枝。
給定目標稀疏模式,剪枝/稀疏化模型可以被視為兩個獨立的問題:
準確率 - 如何找到一組滿足目標稀疏模式的稀疏權重,以最小化模型的準確率下降?
效能 - 如何加速稀疏權重以進行推理並減少記憶體開銷?
我們的工作流設計為兩個部分,分別獨立地回答這兩個問題:
一個前端 Python 使用者介面 API,用於為任何任意稀疏模式查詢稀疏權重。
一個後端稀疏核/操作集合,用於減少記憶體/延遲。
這兩部分之間的交接點是將稀疏權重以密集格式儲存,並將缺失元素的位置填充為 0。這是一個自然的交接點,因為稀疏矩陣乘法和使用該張量的密集矩陣乘法在數值上是等價的。這使我們能夠為使用者提供清晰的後端介面,針對給定的稀疏模式:
如果您能將您的密集矩陣轉換為 **2:4 稀疏格式**,我們可以在沒有數值損失的情況下,將矩陣乘法速度提高 **1.7 倍**。
這還允許使用者利用我們快速的稀疏核,即使他們現有的稀疏權重已經是密集格式。我們預計許多使用者會提出自己定製的前端掩碼解決方案,或者使用其他第三方解決方案,因為這是一個活躍的研究領域。
下面,我們提供一個使用我們的 PyTorch API 加速具有 2:4 稀疏性和 bf16 的模型的示例。
import torch
from torch.sparse import to_sparse_semi_structured, SparseSemiStructuredTensor
from torch.ao.pruning import WeightNormSparsifier
# bfloat16 CUDA model
model = model.half().cuda()
# Accuracy: Finding a sparse subnetwork
sparse_config = []
for name, mod in model.named_modules():
if isinstance(mod, torch.nn.Linear):
sparse_config.append({"tensor_fqn": f"{name}.weight"})
sparsifier = WeightNormSparsifier(sparsity_level=1.0,
sparse_block_shape=(1,4),
zeros_per_block=2)
# attach FakeSparsity
sparsifier.prepare(model, sparse_config)
sparsifier.step()
sparsifier.squash_mask()
# now we have dense model with sparse weights
# Performance: Accelerated sparse inference
for name, mod in model.named_modules():
if isinstance(mod, torch.nn.Linear):
mod.weight = torch.nn.Parameter(to_sparse_semi_structured(mod.weight))
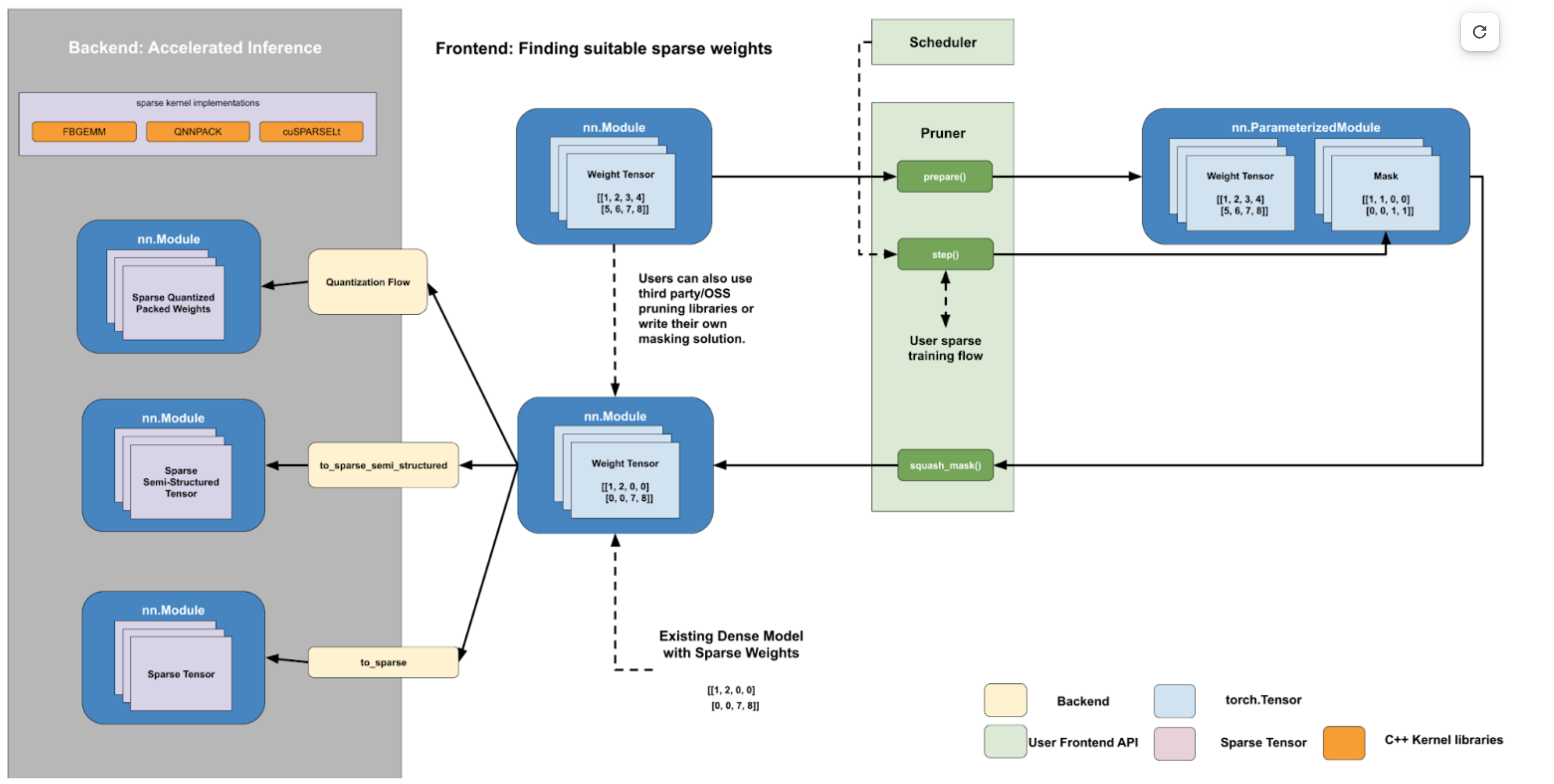
從根本上說,流程是透過操作 torch.Tensors 來實現的。在前端,我們在 sparse_config 字典中透過張量的完全限定名稱指定張量。前端設計遵循量化 API,有一個 prepare 函式,它將 FakeSparsity 引數化附加到 config 中指定的張量上。
FakeSparsity 是一種引數化,它模擬非結構化稀疏性,其中每個元素都有一個掩碼。因此,我們可以使用它來模擬我們想要的任何稀疏模式。
使用者將使用自己的自定義程式碼訓練準備好的模型,並在必要時呼叫 .step() 來更新掩碼。一旦他們找到合適的掩碼,他們將呼叫 squash_mask() 將掩碼融合到權重中,建立一個在正確位置帶有 0 的密集張量。
使用者隨後將透過使用量化流程進行量化塊稀疏 CPU 推理,或者呼叫指定權重張量上的 to_sparse_semi_structured 來轉換他們的模型以進行加速稀疏推理。
背景¶
本節將介紹神經網路剪枝/稀疏性的一些背景知識,以及一些常見剪枝/稀疏性術語的定義。在學術界/工業界,**剪枝**和**稀疏性**經常被互換使用,指代同一件事。這可能會造成混淆,尤其是因為稀疏性是一個被過度使用的術語,它可以指代許多其他事物,例如稀疏張量表示。
請注意,本節側重於**剪枝**,而不是**稀疏訓練**。區別在於,在**剪枝**中,我們從一個預訓練的密集模型開始,而在**稀疏訓練**中,我們從頭開始訓練一個稀疏模型。
為避免混淆,我們通常嘗試使用稀疏性來指代張量。請注意,稀疏張量可以指代包含許多零值的密集張量,或者使用稀疏表示儲存的張量。我們將該流程描述為**剪枝**,將產生的模型描述為**剪枝模型**。
大體上,實現更最佳化的剪枝模型的流程如下:

剪枝的總體思想是,我們可以掩蓋掉一個已訓練神經網路的某些權重,並恢復任何準確率損失。由此產生的剪枝模型可以在利用這種稀疏性的最佳化核上執行,以實現加速推理。
預設情況下,將剪枝引數歸零不會影響模型的延遲/記憶體開銷。這是因為密集張量本身仍然包含剪枝的元素(零值元素),並且在矩陣乘法期間仍會使用這些元素進行計算。為了實現效能提升,我們需要將我們的密集核替換為稀疏核。
廣義來說,這些稀疏表示允許我們跳過涉及剪枝元素的計算,以加速矩陣乘法。為此,這些最佳化的稀疏核在儲存格式更高效的稀疏矩陣上工作。一些稀疏張量佈局與特定後端(如 NVIDIA 2:4)緊密耦合,而另一些則更通用,並被多個後端支援(CSC 被 FBGEMM 和 QNNPACK 支援)。
| 名稱 | 描述 | 稀疏矩陣的儲存方式 |
| COO (sparse_coo) | COOrdinate (座標) 格式用於儲存稀疏矩陣。矩陣儲存為非稀疏資料向量和這些元素在密集矩陣中的索引位置的組合。 | 稀疏矩陣 = {索引:座標位置張量,資料:對應於索引位置的值張量} |
| BSR (sparse_bsr) | 塊稀疏行 (Block sparse row) 格式用於儲存稀疏矩陣。矩陣儲存為資料塊,以及這些塊在密集矩陣中的索引位置。與 COO 非常相似,不同之處在於單個數據由塊而不是標量組成。 | 稀疏矩陣 = {索引:座標位置張量,二維用於矩陣,資料:對應於索引位置的塊張量},其中塊是對應於稀疏模式的矩陣。 |
| CSR (sparse_csr) / CSC (sparse_csc) | 壓縮稀疏行/列 (Compressed sparse row/column) 格式用於儲存稀疏矩陣。稀疏矩陣儲存為列/行上的資料塊,以及這些行/列在密集矩陣中的索引。這是儲存塊稀疏矩陣最緊湊的格式。 | 稀疏矩陣 = {索引:一維列索引張量,IndexPtr:一維張量,指定行對應的列的開始和結束索引,從行 0 開始,資料:對應於索引位置的塊張量。} |
| NVIDIA 2:4 壓縮表示 | 自定義 NVIDIA 壓縮儲存格式,用於 2:4 半結構化稀疏性。我們將稀疏矩陣儲存為壓縮的密集矩陣(尺寸減半),其中包含非剪枝元素和一個位掩碼索引。當我們將稀疏矩陣乘以另一個密集矩陣時,我們使用掩碼來索引密集矩陣並與我們的壓縮密集矩陣相乘。 | 稀疏矩陣 = {位掩碼:剪枝元素的 2 位索引,壓縮密集矩陣:包含所有非剪枝元素,尺寸是原始密集矩陣的一半} |
表 4.1:常見稀疏張量佈局概述。
雖然剪枝的總體思想很簡單,但在成功剪枝模型之前,使用者需要弄清楚許多細節。
這些可以大致分為以下幾類:
剪枝配置 - 我應該剪枝哪些層?我應該剪枝到什麼稀疏級別?
剪枝標準 - 我應該如何決定移除哪些引數?
剪枝策略 - 一旦我移除了引數,我該如何恢復準確率損失?
稀疏模式 - 我在剪枝模型時應該嘗試使用特定的稀疏模式嗎?不同的硬體後端支援不同稀疏模式的加速推理。
剪枝配置¶
神經網路中的所有層並非都一樣。有些層對剪枝可能比其他層更敏感。使用者必須決定要剪枝哪些層,以及每個層的**稀疏級別**,即該權重張量的零值百分比。剪枝配置對剪枝模型的準確率和加速效果都有影響。
確定給定模型的最佳剪枝配置和稀疏級別是一個開放性問題,不存在通用解決方案。這部分是因為最優剪枝配置依賴於後續的剪枝標準和策略,並且存在無數種決定如何剪枝模型以及如何恢復丟失準確率的方法。
確定要剪枝的層及其程度的一種常用方法是執行敏感性分析,方法是:在不同稀疏級別下剪枝模型中的每個層,並檢視隨後的準確率下降(無需重新訓練)。這為使用者提供了每個層的稀疏度-準確率曲線,使用者隨後可以使用該曲線作為代理來確定最佳剪枝配置。
剪枝標準¶
使用者必須決定從神經網路中移除引數的標準。與確定最佳剪枝配置類似,確定最佳剪枝標準是一個開放的研究問題,並且依賴於上述其他因素。
最常見的剪枝標準是使用權重幅度。其思想是,低幅度權重對模型輸出的貢獻小於高幅度權重。如果我們想移除引數,我們可以移除絕對值最小的權重。
然而,即使使用簡單的剪枝標準(如權重幅度),使用者也需要考慮其他因素:
區域性 vs. 全域性範圍
區域性範圍意味著掩碼僅根據層統計資訊進行計算。
優點:掩碼計算簡單。
缺點:準確率與稀疏度權衡可能不是最優的。
全域性範圍意味著稀疏統計資訊不受單個層限制,但如果需要,可以跨越多個層。
優點:無需設定每層閾值。張量統計資訊在層之間共享,並使用層間歸一化來實現。
缺點:計算掩碼時複雜度增加。
用於掩碼計算的張量
權重:僅使用權重張量來計算掩碼。此方法對推理來說最簡單,因為權重張量是恆定的。
梯度:基於權重和梯度範數計算重要性。常用於預訓練方法。目前 CTR_mobile_feed 使用基於梯度的剪枝演算法。
啟用:在一些研究論文中,與目標權重相對應的啟用的範數被用於計算重要性得分。
原地或非原地掩碼更新
原地更新透過執行 W = W * (Mask) 來更新稀疏張量。一旦權重張量被更新,稀疏值將被歸零,無法恢復。
優點:只需要儲存稀疏張量的一個副本(+掩碼)。
缺點:一旦掩碼應用於權重,權重就會被歸零,所有過去的歷史都將丟失。這些權重無法再生。
非原地更新不直接修改張量,而是執行以下操作:W' = W * (Mask) and dW' = dW * (Mask)。
優點:原始張量得以保留(掩碼元素不透過反向傳播更新)。如果掩碼發生變化,權重可以再生。這對於 PAT 是必需的。
缺點:除了未掩碼的權重 (W) 外,還會計算掩碼的權重 (W'),並在記憶體中保留用於前向/後向計算。
| 名稱 | 描述 | 注意事項 |
| 幅度 / 重要性 | 移除範數最小的引數(通常使用 L1)。 | 已被證明在 2:4 半結構化稀疏性下效果良好。透過在一次性幅度剪枝後重複訓練迴圈,可以實現與原始模型相同的準確率。 |
| 移動剪枝 | 這些方法旨在利用梯度資訊來決定移除哪些引數。其思想是移除在微調過程中變化不大的引數。 | 常用於預訓練模型。 |
| 低秩分解 | 這些方法旨在用 SQx 替換 Wx,其中 S 和 Q 是低秩矩陣。 | 通常,這些方法使用某種層級重建,即不透過訓練模型來恢復丟失的準確率,而是尋求匹配層級統計資訊(找到 SQx,使得 L2(SQx, Wx) 最小化)。 |
| 隨機 | 隨機移除引數。 |
表 4.2:一些常見剪枝標準的描述。
剪枝策略¶
這是一個通用術語,描述了使用者嘗試恢復其剪枝模型的準確率下降的方法。在剪枝模型後,通常會看到模型的準確率下降,因此使用者通常會重新訓練剪枝模型以進行糾正。剪枝策略還決定了在模型訓練期間何時以及多久進行一次剪枝。
剪枝策略和剪枝標準之間的界限並不明確,尤其是在剪枝感知訓練方法的情況下,這些方法會在訓練期間更新掩碼。我們有時使用**剪枝** **演算法**這個術語來指代這兩項的組合。這兩個因素以及剪枝配置最終決定了剪枝模型的最終準確率。
| 剪枝策略 | 描述 | 注意事項 |
| 零次迭代 | 剪枝一次,不重新訓練模型。 | 這些方法依賴於更復雜的剪枝標準。 這在文獻中有時被稱為一次性剪枝,但我們將一次性剪枝定義為剪枝一次並重新訓練一次。 |
| 一次性 | 剪枝一次,重新訓練模型一次。 | NVIDIA 已證明,一次性 2:4 半結構化稀疏剪枝在各種常見的視覺/NLP 模型上都能很好地泛化。 \ \ 重訓練策略是簡單地再次重複訓練過程。 |
| 迭代 | 剪枝模型,重新訓練,重複。 | 我們可以迭代地增加稀疏級別,或迭代地剪枝模型中的不同層。 |
| 剪枝感知訓練 | 在訓練期間學習掩碼。 | CTR_feed 目前的剪枝演算法使用的就是此方法。 |
| NAS / 多掩碼 | 訓練期間使用多個掩碼。這可以被視為一種神經架構搜尋。 | PySpeech (FastNAS) 使用。 |
| 層級重建 | 與使用損失函式進行重新訓練不同,我們試圖透過使用類似於知識蒸餾的雙模型方法來儘可能多地從每個層恢復資訊。 | 參見 https://arxiv.org/pdf/2204.09656.pdf |
表 4.3:一些常見剪枝策略的描述。
稀疏模式¶
稀疏模式描述了剪枝的引數在模型/張量內的排列方式。
請記住,通常需要使用最佳化的稀疏核才能實現效能提升。根據權重張量的格式和稀疏級別,稀疏矩陣乘法可能比其密集對應項更快。如果張量不夠稀疏,它也可能更慢。
在最普遍的層面上,剪枝是非結構化的——每個引數都有自己的掩碼。這提供了最大的靈活性,但需要非常高的稀疏度(>98%)才能提供效能優勢。為了在較低的稀疏級別提供加速推理,硬體後端增加了對特殊稀疏模式的支援。
我們尋求以模型剪枝的方式,使權重張量呈現與我們的推理後端相同的稀疏模式。如果我們能夠恢復丟失的準確率,同時保持稀疏模式,我們就可以在稀疏硬體上以加速推理的方式執行該模型,而不會有準確率損失。我們也可以在目標後端上執行以不同稀疏模式剪枝的模型,但會犧牲一些額外的準確率損失。
具體的後端硬體及其對應的稀疏模式,以及剪枝配置,最終決定了我們觀察到的效能加速效果。如果我們使用不同的剪枝標準來剪枝模型,如果它遵循相同的稀疏模式和稀疏級別,它將具有相同的效能特徵。例如,如果我們決定移除幅度最高的權重而不是幅度最低的權重,我們預計這不會改變剪枝模型的效能特徵。
| 稀疏模式 | 掩碼視覺化
(50% 稀疏級別) |
||||||||||||||||||||||||||||||||
| 非結構化稀疏性 |
|
||||||||||||||||||||||||||||||||
| 2:4 半結構化 |
|
||||||||||||||||||||||||||||||||
| 塊稀疏性 |
|
||||||||||||||||||||||||||||||||
| 結構化稀疏性 |
|
表 4.4:一些常見稀疏模式的描述。
有關我們支援的 API 和基準測試的更多資訊,請參閱 稀疏性 README。
